[알고리즘] 2차원 점군을 감싸는 최소면적의 직사각형 그리기(작성중)

본 과정은 Convex Hull과 Rotating Caliper 알고리즘을 학습해 가는 과정입니다.
결론만 얻고 싶은 분은 다른 분의 포스팅을 참고하시길 추천드립니다.

 

페이스북에서 우연히 읽게 된 질문글이다.

2차원 평면상에 수십여개의 점이 있을 때,
이 점을 모두 포함하는
최소 면적의 직사각형 그리는 방법?

 

여러가지 해법이 있겠지만,
(막연하게나마 Convex Hull과 Rotating Caliper 알고리즘에 대해선 들은 적이 있었다.)
아주 단순한 방식을 들어 풀 수 있을 것 같다는 생각이 들었다.

아래와 같은 점군이 있다고 가정하자.

대략 아래처럼 직사각형이 그려져야 한다.

직사각형이 회전하지 않아도 된다는 가정하에는
그냥 x_min, x_max, y_min, y_max 네 점을 찾아서 직사각형을 그리면 그만이겠지만,
위 그림처럼 직사각형이 회전을 한다면?
그 때는 먼저
가장 긴 축을 찾아내야 한다.

우선 두 점간의 거리를 리턴하는 함수를 하나 만들고,

from math import sqrt

def dist(dot1, dot2):
    return sqrt((dot2[0] - dot1[0]) ** 2 + (dot2[1] - dot1[1]) ** 2)

모든 점끼리 비교하면서(2중for문이라 좀 느리다는 게 흠ㅜ)
점간 거리가 최대가 되는 두 점인 target을 찾는다.

dot_list = list(zip(xs, ys))

max_length = 0
target = []
for i in dot_list:
    for j in dot_list:
        if i == j:
            continue
        elif dist(i, j) > max_length:
            max_length = dist(i, j)
            target = [i, j]
print(target, max_length)

이 두 점 사이의 선분 a가 직사각형의 긴 축이 된다.

plt.scatter(xs, ys)
plt.plot(list(zip(*target))[0], list(zip(*target))[1], c="r")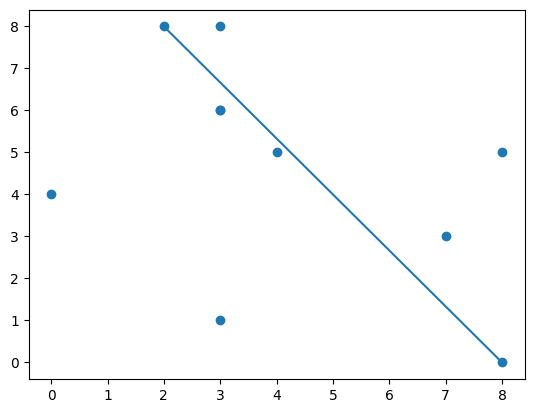

그 다음은 저 선분과 수직하는 축방향으로 아래위 가장 먼 점 두 개를 찾은 후,
두 점을 지나면서 선분a와 평행하는 두 선분을 그려 이으면 
우리가 그리고자 하는 최종 직사각형이 될 것이다. 

거의 다 풀렸다.
직선의 방정식 또는 직선 내 두 점을 알 때,
그 직선과 한 점b의 최단거리를 구하려면?

굳이 선형대수나 기하학을 모르더라도
ChatGPT에게 물어보면 되잖아?

빨간색 네모 안의 아이콘을 클릭하면 코드가 만들어져 있음

그런데 나는 위로 아래로 부호가 달라야 하니까 한 번 더 물어봤다.

방향을 알아야 하니까, 부호도 필요하다. 다행히 abs만 빼면 된다.

 

위 답변에서 ChatGPT가 알려준 최종 코드는 아래와 같다.

from math import sqrt

def shortest_distance_with_sign(x1, y1, x2, y2, x0, y0):
    """
    Calculates the shortest distance from a line passing through points (x1, y1) and (x2, y2)
    to a point (x0, y0). Returns the distance with a sign (+/-) indicating whether the point 
    is above (+) or below (-) the line.
    """
    # Calculate coefficients A, B, and C for the line equation Ax + By + C = 0
    A = y2 - y1
    B = x1 - x2
    C = x2 * y1 - x1 * y2

    # Calculate the signed distance
    numerator = A * x0 + B * y0 + C
    signed_distance = -numerator / sqrt(A**2 + B**2)
    return signed_distance

# Test the function with the same example points
# 0,0과 10,0을 지나는 직선에서 점(0,10)과의 거리
shortest_distance_with_sign(0,0,10,0,0,10)
# == 10

한 번에 잘 대답해줘서 다행히 시간을 아꼈다.

이제 모든 점을 돌면서 max와 min 값만 찾으면 되겠다.
(약간 변환과정은 필요하겠지만 ChatGPT와 함께라면 두려울 것도 없다.)

dist_list = []
for i, j in list(zip(xs, ys)):
    dist_list.append(shortest_distance_with_sign(*target[0], *target[1], i, j))

print(max(dist_list), min(dist_list))

그러자 위로 3.0, 아래로 -4.0 이라는 숫자가 나왔다.

하여튼 이런저런 과정(아래 기술할 것)을 거쳐서 최종 실행화면은 아래와 같다.

오예!

 

헉, 잘못됐다!ㅜ

이런 극단적인 경우를 시도해 보니 잘못돼 있다는 게 보인다...ㅜ
첫코부터 잘 못 꿰었구나.

사실상 최대면적의 직사각형이다!ㅜㅜㅜㅜㅜㅜㅜㅜㅜ

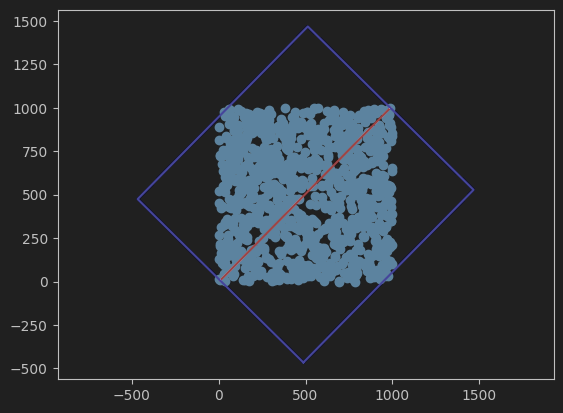
역시 ConvexHull과 Rotating Calipers 알고리즘을 쓰는 방법 밖엔 없나 싶다ㅜㅜㅜㅜㅜㅜ
지금까지 작성한 알고리즘을 개선하는 시도보다는(회전해보면 될 것 같긴 한데),
깔끔하게 정석 알고리즘으로 구현하는 게 훨씬 나아 보인다.

이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...
이건 시간낭비가 아니었어...

 

그럼 도대체 Convex Hull은 뭐고 Rotating Caliper는 뭐길래?

(...계속)